数理科学プログラム
数理科学への深い理解に基づいた洞察力・論理的思考能力を涵養する教育を実施します。これにより,数学のみならず,自然や社会の諸現象の数理科学的な構造を捉えて,社会の諸課題の解決を行うことができる人材の養成を目的とします。
プログラムの概要
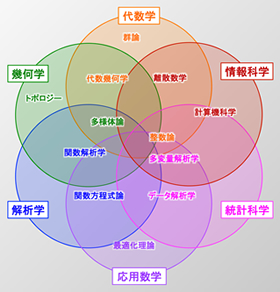
「数理科学」とは,伝統的な純粋数学を核としながらも,科学技術の発展や社会構造の変革に関わる応用数学をも内包する基礎科学の一大領域を指します。数理科学プログラムでは,数・式・図形の概念を一般化・抽象化していく過程を通して,論理的思考力・科学的分析力・創造的発想力を涵養します。また,これらの能力を基礎に,現実世界の現象理解や状況判断を行うための科学的推論能力を養成します。その上で,これらの力を発展的に融合させることにより,社会のさまざまな領域で高度専門職業人として活躍できる人材を育成します。他の学問の基盤となるだけでなく,数学やそれを含む数理科学自身が興味深い対象の集合体であることを訴えていきます。
学ぶこと
数理科学プログラムでは,プログラムの教育目標を達成するために,以下の基本方針にしたがって教育課程を定めます。

- 文系理系の違いにとらわれずさまざまな学問分野に興味と関心を持たせるとともに,数理科学の世界に閉じこもることなく,他分野との協調・他分野への応用について意識を広げさせます。そのために,教養科目における自然・科学の分野以外からの履修や,理工共通科目における他の自然科学や工学系からの履修を奨励します。
- プログラムの基幹教育は,高大接続から大学院への展開までを視野に入れ,基盤の充実を第一に考えます。そのために,科目数を絞ってスタンダードな内容を確実に修得させます。
- 初年次からの微分積分と線形代数はすべての分野の基礎となるので,徹底して数学の考え方を身につけさせます。
- プログラムの基幹教育においては,数理科学を6分野(代数学,幾何学,解析学,応用数学,統計科学,情報科学)から構成されると考え,それぞれを同等の重みで扱い同数の科目を設置します。各分野とも包括的な内容を含む科目を配置してすべての学生に修得させます。学生は3年次以降に自身の興味に応じて専門を絞っていくことになりますが,個々の分野が相互に影響しあって数理科学というひとつの構造物が構築されていることを認識し,主専攻分野以外にも努めて第二,第三の分野にも関心を広げるように奨励します。
- 社会生活への順応,学術上の国際化に配慮して,将来設計や英語の利用を目的とした科目を配置します。社会における科学の役割と影響力を理解し,複雑化する社会を生き抜くために自ら学び続けられることが必要だからです。同時に国際化社会を生き抜くために,言語を通して情報を受信する能力,発信する能力を養成します。
養成する人材像
論理的思考力と発見的創造力をあわせもち,数理的知識・推論を活用して問題解決に寄与するとともに,次の世代の発展にも貢献できる科学者,技術者,教育者,研究者。
Pick Up 研究テーマ紹介
坊向 伸隆 准教授
研究テーマ微分可能多様体
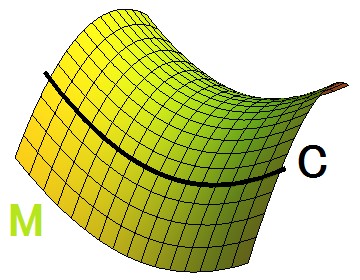
滑らかな曲線Cを考えます。その曲線を微分して接ベクトルを導出し,その接ベクトルの長さを積分すれば,曲線の「長さ」という量が得られます。このような計算をさらに続けると曲線の「曲率」や「捩率」といった量も得られることになります。滑らかな曲面Mについても同様で,それに解析的演算や代数的演算を施せば,曲面の「ガウス曲率」や「平均曲率」といった量が得られます。微分可能多様体とは滑らかな曲線や曲面の概念を一般化したものであるため,微分可能多様体上では代数学,位相数学,解析学などの理論が展開されることになります。代数学,位相数学,解析学といった分野にとらわれることなく純粋数学を楽しみたい方へ微分可能多様体はおすすめです。
- その他の研究テーマ
-
- リー群の関数空間における表現理論
- 等質空間の分類理論
